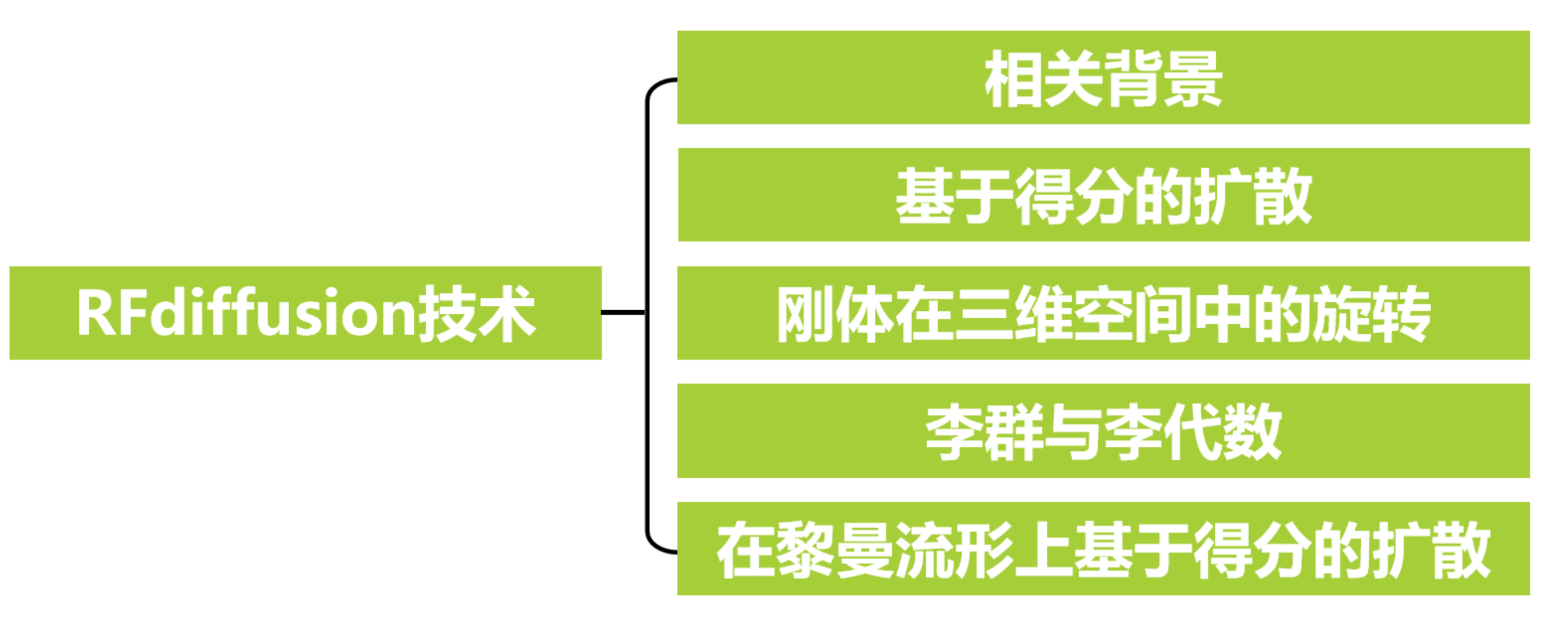
本文内容速览:
相关背景
然而,传统抗体生产虽然成就显著,却也暴露出一些固有局限性。首先,传统抗体的生产高度依赖于哺乳动物细胞系统。这一过程不仅成本高昂、耗时较长,还受限于培养条件与生物反应器的技术瓶颈,难以实现大规模生产。其次,即便是同一批次的传统抗体生产,也难以避免批次间微小差异的存在。这些不一致性源于生物体系内的自然变异、培养条件的微调以及收获和纯化过程中的技术波动。再次,传统抗体因其复杂的三级和四级结构,在特定条件下容易发生变性或降解,这限制了其在某些环境下的有效性和长期储存能力。
正是在探索克服这些挑战的过程中,科学家们将目光转向了自然界中一个小小的灵感——“小肽”(small peptides)。“小肽”这一类长度限定于150个氨基酸以下的多肽片段,自上个世纪以来便吸引了科学家们的浓厚兴趣。尽管其结构已被成功解析,并展现出独特的晶体形态,但对于它们在生物体内的具体功能及作用机制,至今仍有许多未解之谜等待着科学界的深入探究。
小肽的价值不仅在于填补了生物学知识空白,更在于其潜在的应用前景。近年来的一项研究成果(Okura et al., 2022)揭示了冠状病毒基因组中编码的alpha螺旋结构小肽片段,这些特定结构的小肽被发现对病毒感染过程具有调节作用,甚至在某些情况下能够抑制病毒活性。这一发现为理解病毒与宿主相互作用机制提供了新视角,并暗示了小肽可能作为抗病毒疗法的新兴方向。
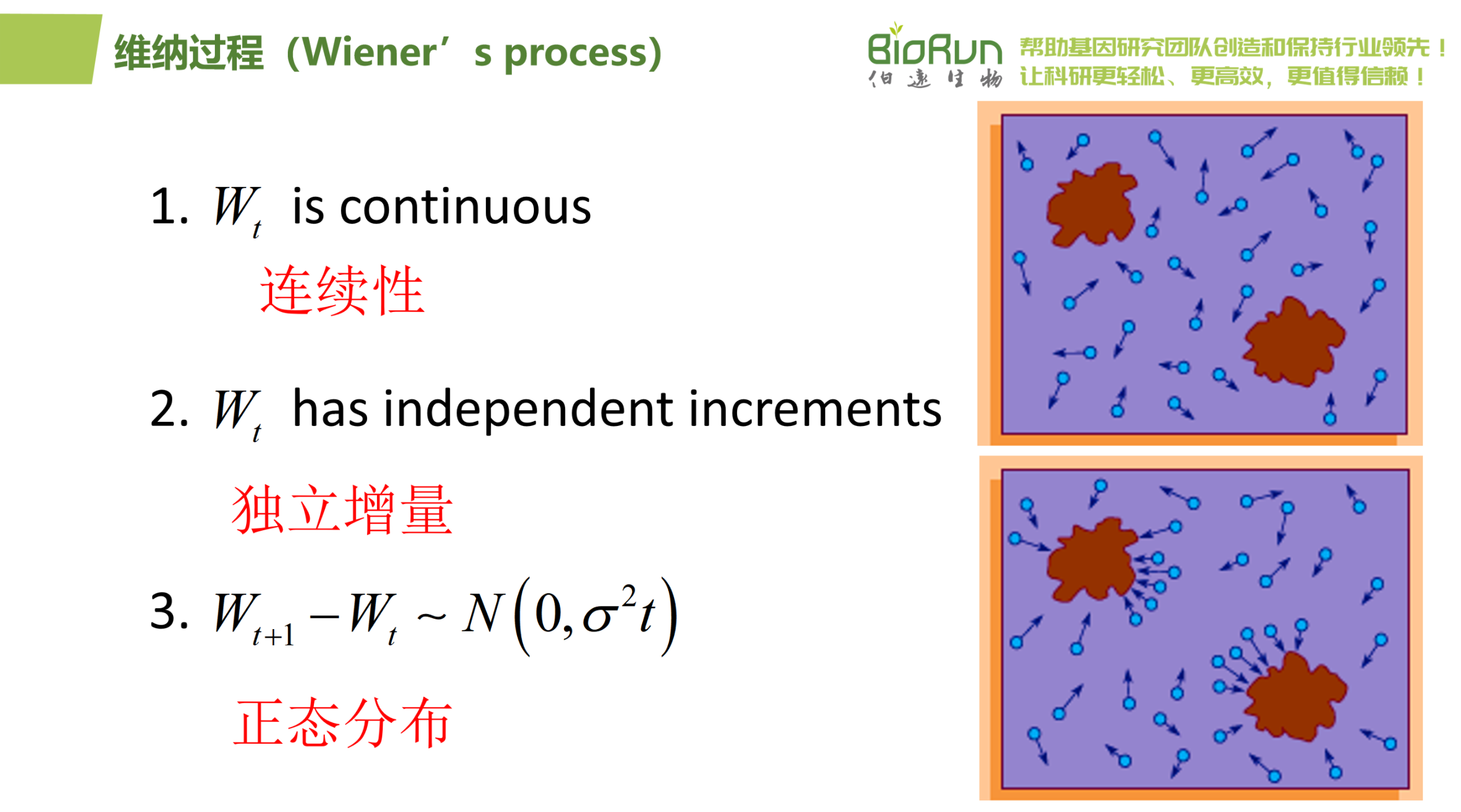
维纳过程,作为概率论和随机分析领域的基石之一,提供了一种描述物体在时间序列中进行连续且无记忆随机移动的理想化模型。其核心特性可归纳为以下三点:
1.连续性:维纳过程中的路径是连续的,这意味着在任意两个时间点之间,物体的位置变化不会出现跳跃或断点,而是平滑过渡。


伊藤积分是一种针对扩散过程的特定类型的随机积分,它允许研究人员对涉及随机变量(如维纳过程)的函数求导和积分。与传统微积分不同的是,伊藤积分考虑了由随机波动带来的额外“噪声”,从而能够更准确地描述那些在现实世界中广泛存在的、受随机因素影响的现象。
基于得分的扩散(score based diffusion modeling,SDM)(Song & Ermon, 2020)是RFdiffusion中用到的扩散模型。去噪概率扩散模型(denoising diffusion probablistic modeling,DDPM)(Ho et al., 2020)是文生图应用StableDiffusion中用到的扩散模型。两者统一在随机微分方程(SDE)框架(Song et al., 2021)中。这里的随机微分方程,指的就是伊藤扩散方程的微分形式。也就是伊藤引理中的形式。
图4 随机微分方程。


想要让Xt成为完全意义上的噪声,只需要系数ā𝑡趋近于零。换言之,噪声的方差是有上界的。这个上界无限趋近于一。因此,DDPM又叫做Variance Preserving模型。
推完前向算法,接着推后向算法。
图7 后向算法一。
图8 后向算法二。


万物皆可神经网络。于是,人们想训练一个神经网络Sθ(x)来估计对数梯度项。从这里开始,将神经网络Sθ(x)叫做score function。用重要性采样(importance sampling)的方法,使得score function接近对数梯度项。第二个问题,真实分布f(x)不可导(intractable)。那可以用一个可导的分布去近似它。最简单的就是正态分布。
图12 分数匹配二。
按说推到这一步,问题就全部解决了。但高斯函数具有一些比较好的性质。于是研究人员继续化简,看看高斯函数近似下的对数梯度项是否能化简成简单优美的形式。果然,对数梯度项最终化简为标准化后的高斯白噪声。
图13 分数匹配三。
至此,得到了完整的扩散模型。
图14 分数匹配四。原图来自jmtomczak.github.io。
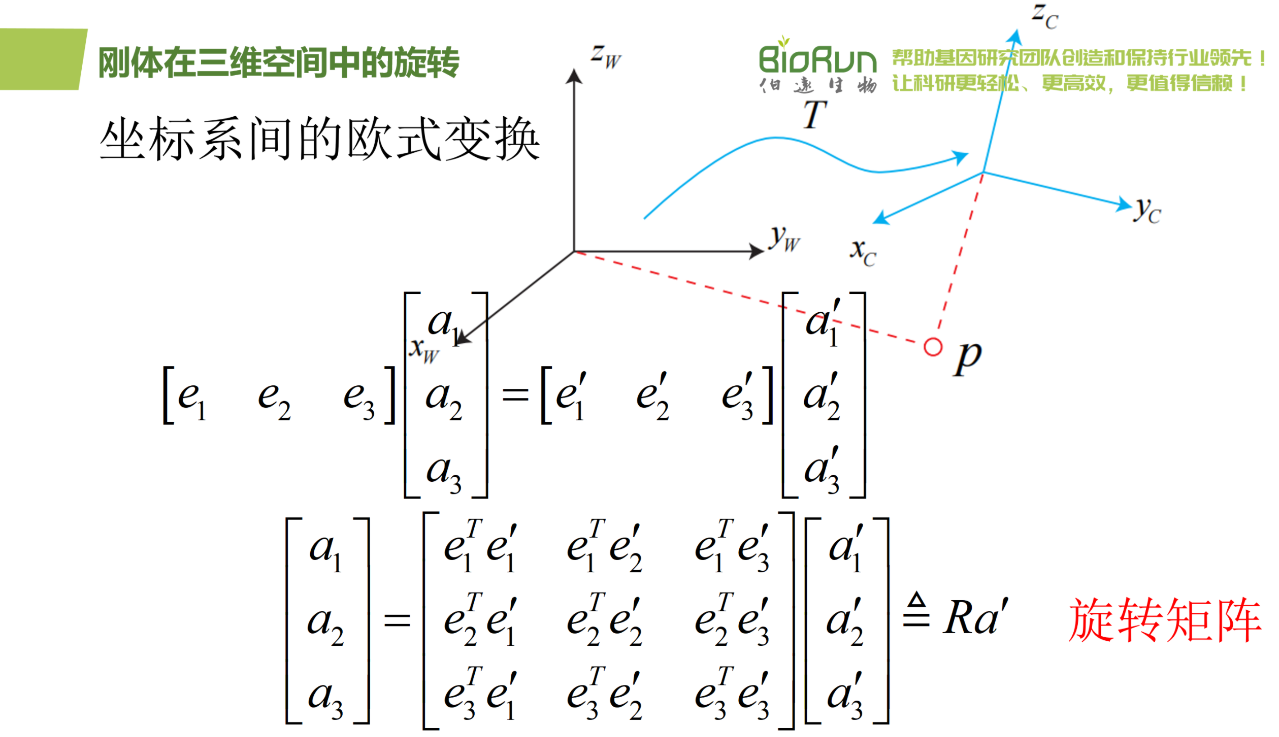
为了描述两个坐标之间的关系,研究人员对上面等式左右同时左乘(e1 e2 e3)。把中间的阵拿出来,定义成一个矩阵R。这个矩阵由两组基之间的内积组成,刻画了旋转前后同一个向量的坐标变换关系。只要旋转是一样的,那么这个矩阵也是一样的。可以说,矩阵R描述了旋转本身。因此它又称为旋转矩阵。
1. 旋转矩阵有九个向量,但一次旋转只有三个自由度。因此这种表达方式是冗余的;
2. 旋转矩阵自身带有约束:它必须是个正交矩阵,且行列式为1。当想要估计或优化一个旋转矩阵时,这些约束会使得求解变得更困难。
因此,研究人员希望有一种方式能够紧凑地描述旋转。例如,用一个三维向量表示旋转,可行吗?答案是肯定的。任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是,可以使用一个向量,其方向与旋转轴一致,而长度等于旋转角。这种向量,称为旋转向量。这种表示方法,称为旋转的轴角表示。
研究人员来将旋转的轴角表示形式化。注意这里是欧式空间。用的是向量表示。给定旋转轴n、向量v、旋转后的向量v’。向量可以分解为与旋转轴平行的分量vⅡ和与旋转轴垂直的平面π内的分量vㅗ。向量v’的垂直分量与向量v的垂直分量之间的夹角大小θ。现在将旋转后的向量v’表示为旋转轴n、旋转角θ和向量v的含量。
图17 反对称矩阵。
可以观察到,轴角表示中轴v’、角θ、轴v之间的关系式是用向量工具进行描述的。计算机中通常是矩阵计算。因此,研究人员的目标是推导出这个关系式的矩阵形式。问题来了。怎样用矩阵乘法表示向量叉乘。这里,用反对称矩阵将向量叉乘表示成矩阵乘法。定义了两个转换符:Λ(读作Hat)和V(读作Vee)。Λ是从向量到反对称矩阵的转换符。V是从反对称矩阵到向量的转换符。
图18 罗德里格斯公式一。
罗德里格斯公式(Rodrigue’s Formula)揭示出旋转矩阵R、旋转向量v和v’之间相互转换的关系。假设有一个旋转轴为n,角度为θ的旋转。显然,它对应的旋转向量为θ·n。
图19 罗德里格斯公式二。
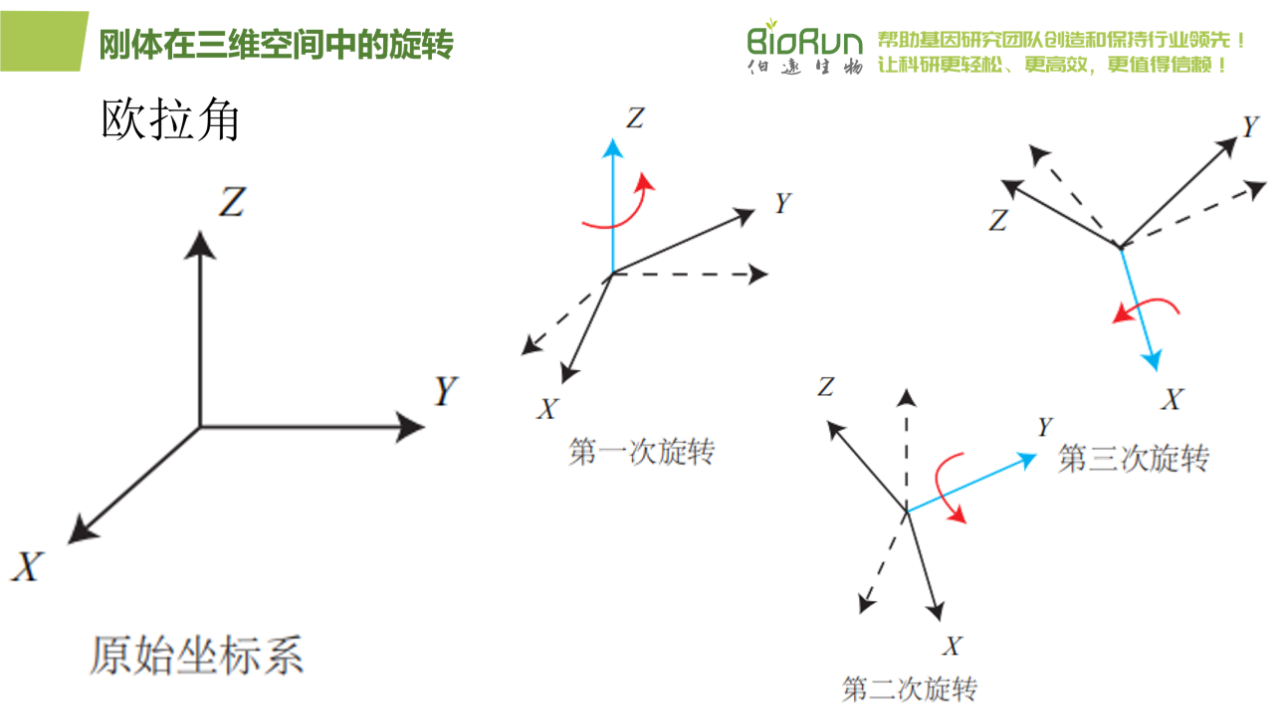
图20 欧拉角一。
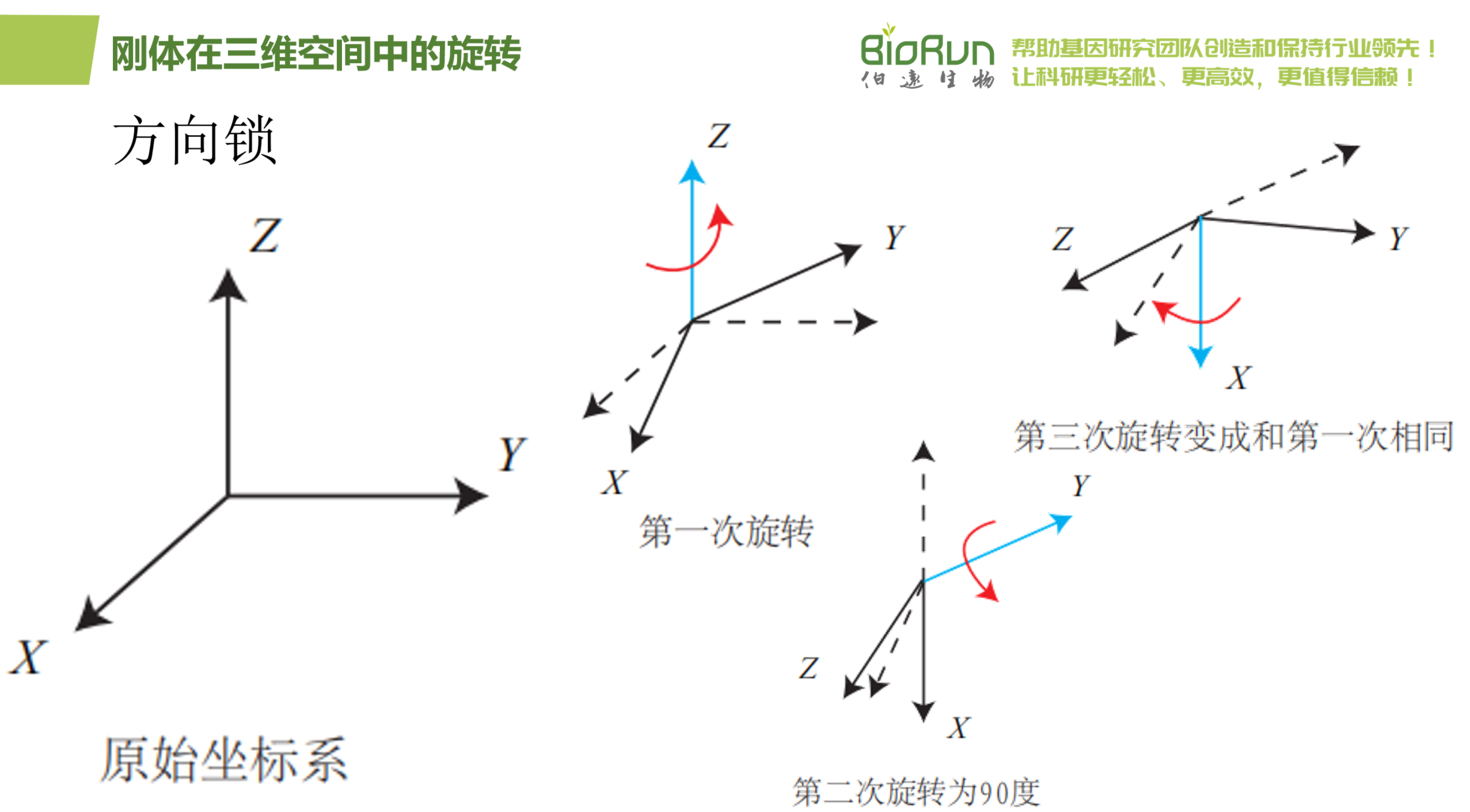
欧拉角的一个重大缺点是会碰到著名的万向锁问题(Gimbal Lock):在俯仰角为±90°时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由三次旋转变成了两次旋转)。这被称为奇异性问题,在其他形式的欧拉角中也同样存在。理论上可以证明,只要我们想用三个实数来表达三维旋转时,都会不可避免地碰到奇异性问题。由于这种原理,欧拉角不适于插值和迭代。
然而,SDM框架包含计算得分(score)的微分运算。故需要引入李代数(Lie algebra)作为李群SO(3)的“微分”,或者说,在单位元附近对SO(3)进行线性化处理。更重要的是,李群与李代数之间的联系并非仅限于抽象理论层面:指数映射(exponential mapping)作为二者间的桥梁,赋予了从线性空间到非线性变换之间转换的能力。通过这一映射,研究人员不仅能够在SO(3)中以向量形式表达角速度、加速度等动态变量,还能将其无缝转化为SO(3)内的具体旋转矩阵。
图23 李群二。
图24 李群三。
图25 李群四。
图26 李群五。
图27 李群六。
图28 李群七。
图29 李群八。
图30 李群九。
图31 李群十。
然而,在将基于得分的扩散模型推广至更为复杂的非欧几何——黎曼流形时,则需面对额外挑战。首先,在前向算法中,由于流形本身可能具有弯曲、拓扑变化等特性,传统的高斯噪声添加与去除策略不再适用。其次,在后向算法中,通过对流形上各点邻域进行局部线性化处理,并在得到的平坦近似空间内计算得分函数的导数。随后借助指数映射,将切平面上获得的结果投射回原始流形,以保持整个扩散路径在几何意义上的一致性和合理性。再次,在进行得分匹配(score matching)时,由于欧几里得空间中定义的梯度算子无法直接应用于曲面数据,研究人员转而寻求以李代数为基础重新构建相应的微分运算体系。通过将传统的微分方程解耦为一系列沿黎曼流形切向量场展开的方向导数组合,并利用矩阵对称性与群论原理重构得分函数表达式,可以有效克服非均匀度量效应带来的计算难题,同时确保了所建立模型在数学上严谨且物理意义清晰。
在本节中,我们将从这三个方面展开,介绍黎曼流形上基于得分的扩散。
图32 R前向一。

图34 R前向三。
图35 R前向四。
图36 R前向五。
图37 R前向六。
图38 R前向七。
图39 R前向八。
图40 R后向。原图来自www.bilibili.com。
图41 R匹配一。
图42 R匹配二。
图43 R匹配三。
图44 R匹配四。
算法实践
HA、IL-7Rα、PD-L1、InsR、TrkA微抗体设计
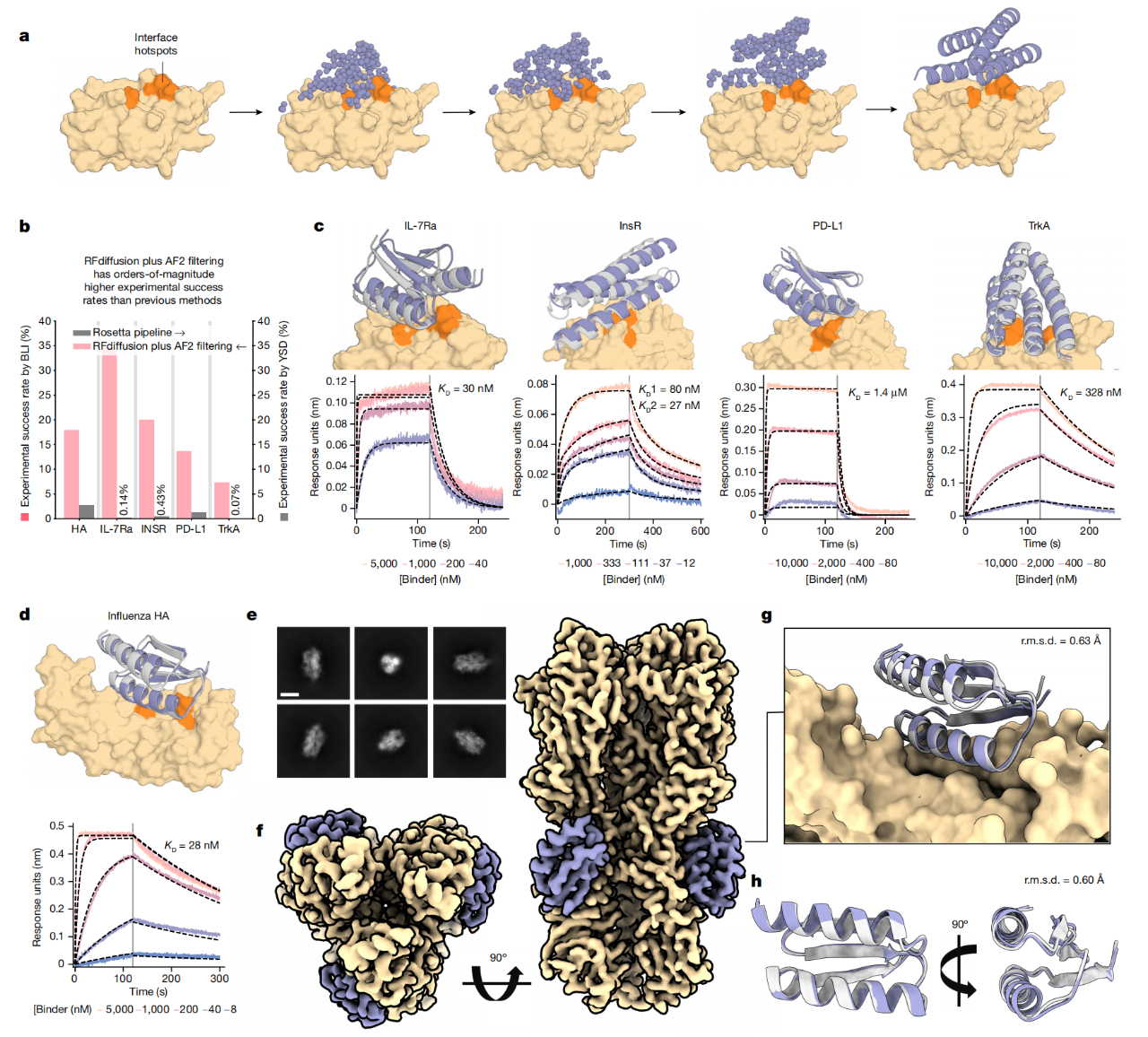
为了比较RFdiffusion与先前的结合蛋白设计方法,作者对五个目标蛋白进行了binder设计:A型流感H1血凝素(HA)、白细胞介素-7受体α亚基(IL-7Rα)、程序性死亡配体1(PD-L1)、胰岛素受体(InsR)和肌动蛋白调节蛋白受体激酶A(TrkA)。对于每个目标,作者设计了潜在的binder,有或没有条件化在兼容的结构折叠信息上,在计算机模拟中取得高成功率。设计通过Alphafold2对接口及单体结构的置信度进行了筛选,并从每个目标中选择了95个设计进行实验评估。
结合界面往往与蛋白质数据库(PDB)中这些目标的接口截然不同。为了评估binder的特异性,通过竞争BLI测试了六个对IL-7Rα亲和力最高的结合蛋白,所有这六种结合蛋白都与一个结构验证过的阳性对照在相同位点上进行了结合竞争。虽然需要进一步的工作来全面描述整个蛋白质组中的特异性,但这些数据初步证实了新设计结合蛋白的高特异性。
图45 实验验证(Watson et al.,2023)。
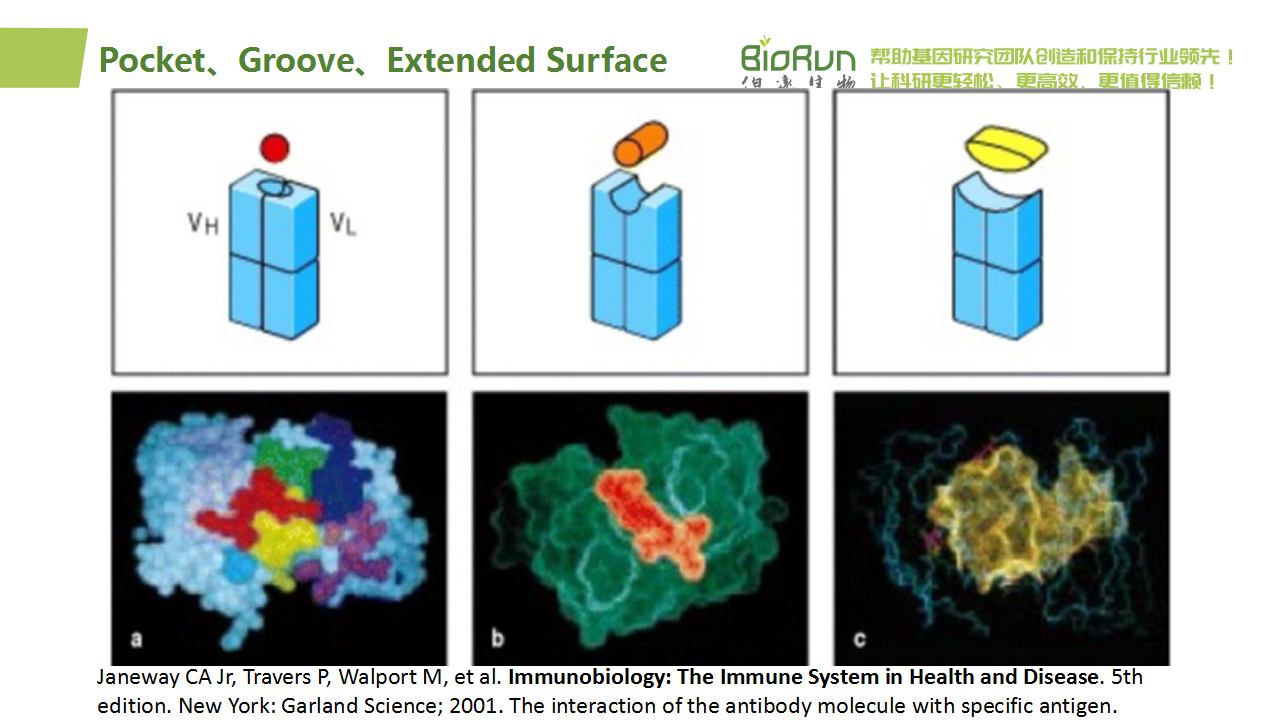
在微抗体设计中,考虑的主要是沟槽型。一方面,groove型接口通常沿抗体或binder分子的表面形成一条较深且细长的沟槽,这一特征使得它在与目标抗原相互作用时具有较高的结构兼容性和空间适应性。相比于pocket型界面要求抗原精确嵌入特定凹洞中,groove型的设计允许更广泛的结合模式和角度调整,从而增加了微抗体对不同形状和大小抗原的识别范围。另一方面,groove型接口往往能提供更为明确且易于操作的接触点。设计者可以聚焦于沟槽内部及周边几个关键氨基酸残基的优化,以增强与目标表位的亲和力,而无需像extended surface那样考虑复杂的二维或三维平面匹配问题(Wu et al., 2023)。这不仅降低了设计难度,也加速了binder开发的速度。
对于沟槽型结合界面,当一个蛋白质(或其特定结构域、肽段等)表现为具有正向曲率的凸起表面时,它的配对分子(例如抗体的一端)将倾向于展示相反的负向曲率——即形成较为凹陷的沟槽,以实现两者间的精准匹配与紧密结合。具体到抗体-抗原识别中,groove型界面通常是指由抗体分子表面形成的一条长而狭的凹槽(groove),它能够与目标抗原上具有特定延伸性或线性特征的部分相匹配。在这种场景下,如果抗原表位展现为曲率正向(凸面)形态,那么为了实现最佳结合状态,相应的抗体groove区域确实应当设计或自然进化出负向曲率(即凹面)以容纳并贴合抗原的这一特征。
当抗原一侧的结合界面是凹面时,用扩散法设计骨架效果较好。而当抗原一侧的结合界面是凸面时,应改用参数化设计方法(parametric groove design)(Yang et al., 2024)。“凹面扩散法”与“凸面参数化策略”代表了两种针对不同表位特征所采用的高效且互补的设计思路。通过细致分析目标表位几何形态及其化学性质,合理选择或组合上述方法将在一定程度上提高微抗体设计的成功率。
图46 展望PPI形状。原图来自教材Immunobiology: The Immune System in Health and Disease。
微抗体设计
进化法则提供了一种更为全面且系统化的思考框架,其关键在于强调在对抗体序列进行优化调整的同时,也需考虑到抗原自身的动态适应性变化。two-sided diffusion(Zhang et al., 2024)策略便是在这一思路指导下应运而生的创新实践之一,尤其适用于处理那些涉及乱序区(disordered regions)或存在构象灵活性的复杂目标对象。通过构建双侧扩散模型并结合机器学习算法分析结果,研究团队能够更加深入地理解微抗体与抗原之间相互作用的动力学特征及稳定状态分布规律。
T. Okura et al., “Hydrophobic Alpha-Helical Short Peptides in Overlapping Reading Frames of the Coronavirus Genome,” Pathogens, vol. 11, no. 8, 2022.
D. Fujiwara and I. Fujii, “Phage selection of peptide ‘microantibodies’.,” Curr Protoc Chem Biol, vol. 5, no. 3, pp. 171–194, 2013.
Grigoryan and W. F. DeGrado, “Probing Designability via a Generalized Model of Helical Bundle Geometry,” Journal of Molecular Biology, vol. 405, no. 4, pp. 1079–1100, Jan. 2011.
J. L. Watson et al., “De novo design of protein structure and function with RFdiffusion,” Nature, vol. 620, no. 7976, pp. 1089–1100, Aug. 2023.
J. Dauparas et al., “Robust deep learning–based protein sequence design using ProteinMPNN,” Science, vol. 378, no. 6615, pp. 49–56, Oct. 2022.
X. Zhou et al., “ProRefiner: an entropy-based refining strategy for inverse protein folding with global graph attention,” Nat Commun, vol. 14, no. 1, p. 7434, Nov. 2023.
M. Gao, D. Nakajima An, J. M. Parks, and J. Skolnick, “AF2Complex predicts direct physical interactions in multimeric proteins with deep learning,” Nat Commun, vol. 13, no. 1, p. 1744, Apr. 2022, doi: 10.1038/s41467-022-29394-2.
F. Homma, J. Huang, and R. A. L. Van Der Hoorn, “AlphaFold-Multimer predicts cross-kingdom interactions at the plant-pathogen interface,” Nat Commun, vol. 14, no. 1, p. 6040, Sep. 2023, doi: 10.1038/s41467-023-41721-9.
Song and S. Ermon, “Generative Modeling by Estimating Gradients of the Data Distribution,” Oct. 10, 2020
Ho, A. Jain, and P. Abbeel, “Denoising Diffusion Probabilistic Models,” Dec. 16, 2020